This page is not compatible with Internet Explorer.
For security reasons, we recommend that you use an up-to-date browser, such as Microsoft Edge, Google Chrome, Safari, or Mozilla Firefox.
Thermal Conductivity Simulation
with VGSTUDIO MAX
Simulate thermal conductivity on CT scans of different materials using the Transport Phenomena Simulation Module for VGSTUDIO MAX.
Simulation of Thermal Conductivity
Thermal conductivity measures a material's ability to allow the transport of heat.
The Transport Phenomena Simulation Module for VGSTUDIO MAX:
- Simulates the stationary temperature and thermal flux fields in a two-component material, where each material has a different thermal conductivity, with the boundary condition that inlet and outlet are connected to heat reservoirs, each at a different constant temperature.
- Works directly on voxel data and makes use of the sub-voxel accurate, local adaptive surface determination in VGSTUDIO MAX.
- Has "experiment mode" for performing a virtual experiment on the transportation of heat, as well as "tensor mode" for calculating the thermal conductivity tensor.
The thermal conductivity module is based on the following differential equations for stationary temperature and heat flux fields in a two-component material
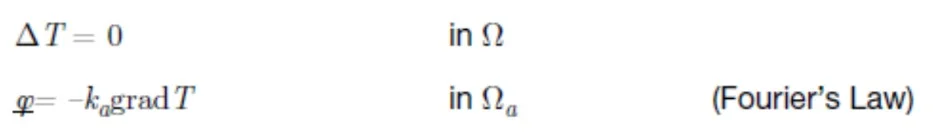
where Ω is the entire simulation domain and Ωₐ is the domain of component a (with a = 1, 2). It is assumed that Ω₁ and Ω₂ do not overlap and their union equals Ω. T is the temperature, φ is the heat flux, kₐ is the thermal conductivity of component a, Δ is the Laplace operator, and grad is the gradient operator.
Experiment Mode
In experiment mode, the software performs a virtual experiment on the CT data of a structure, simulating the transport of heat through the structure from an inlet plane towards an outlet plane parallel to each other. Sealed or embedded boundary conditions perpendicular to the inlet and outlet plane can be defined. A temperature difference must be specified as driving quantity for the flow.
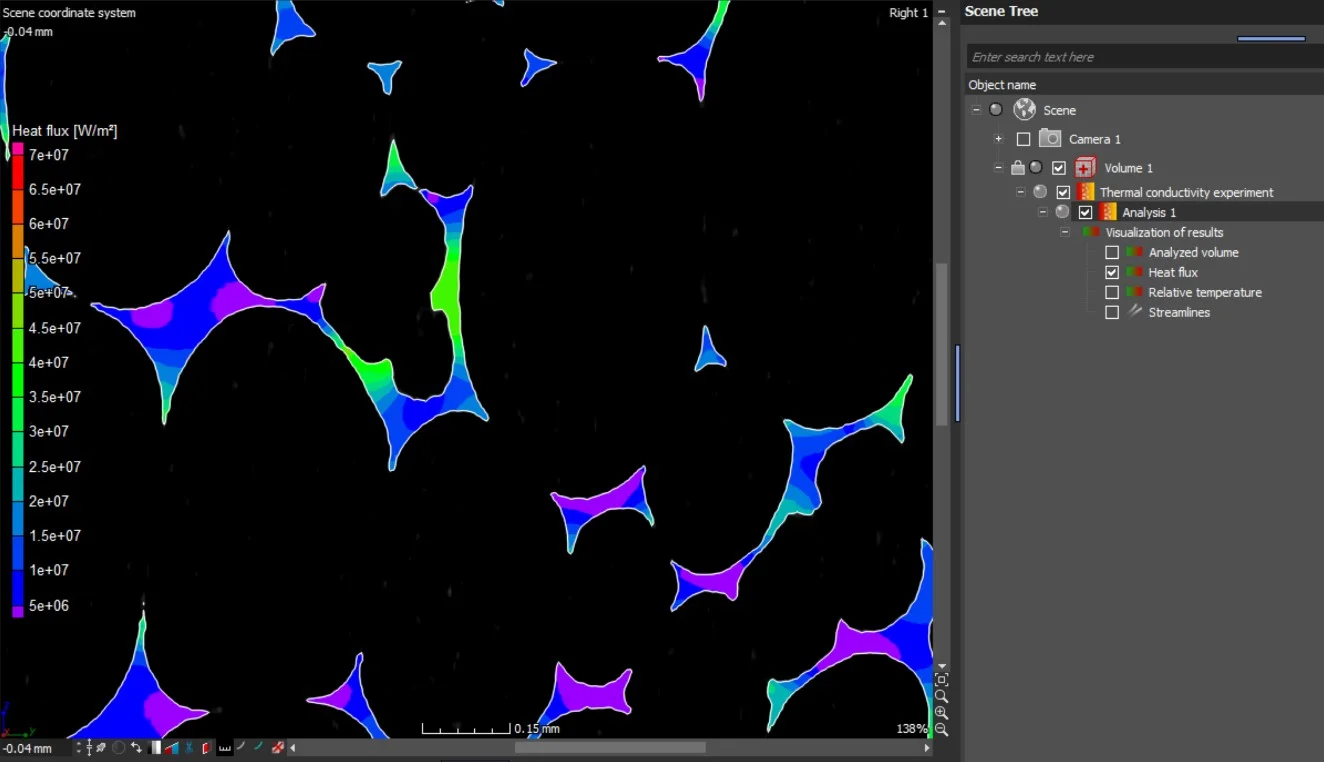
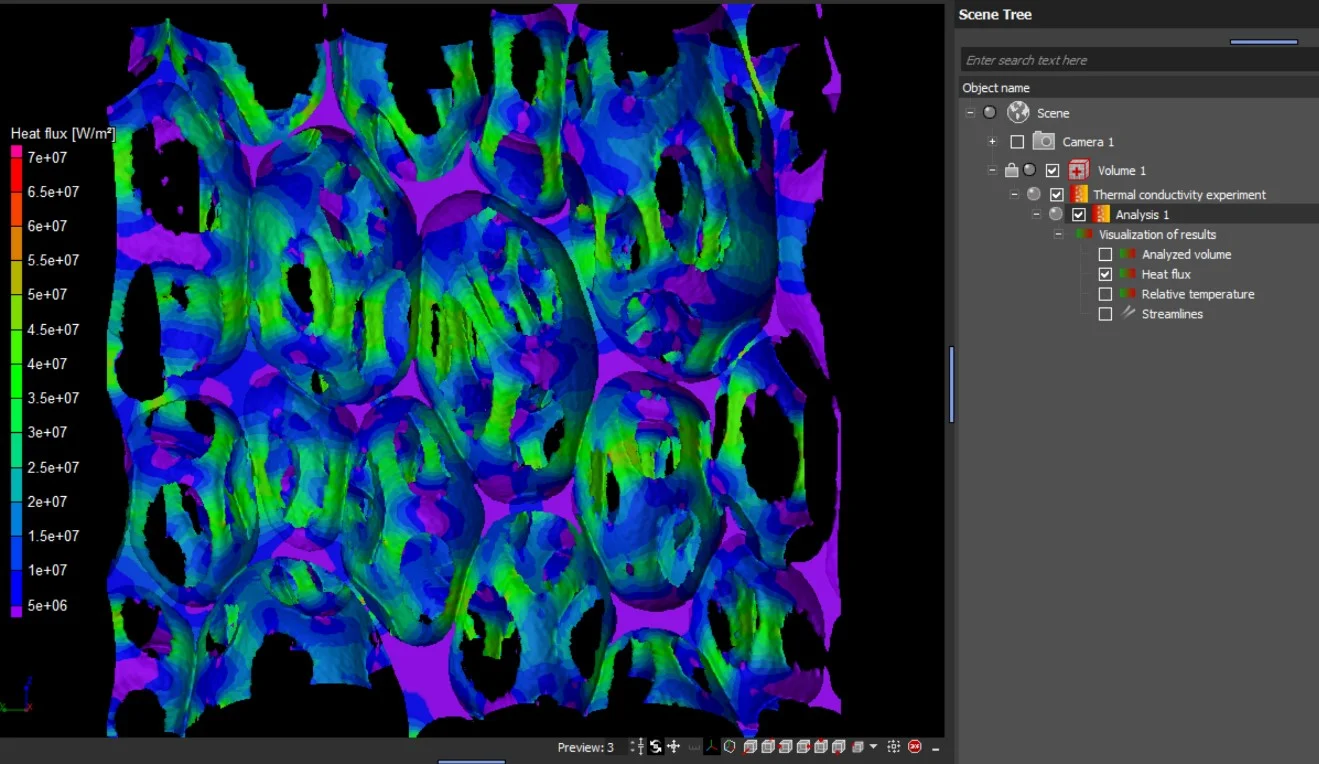
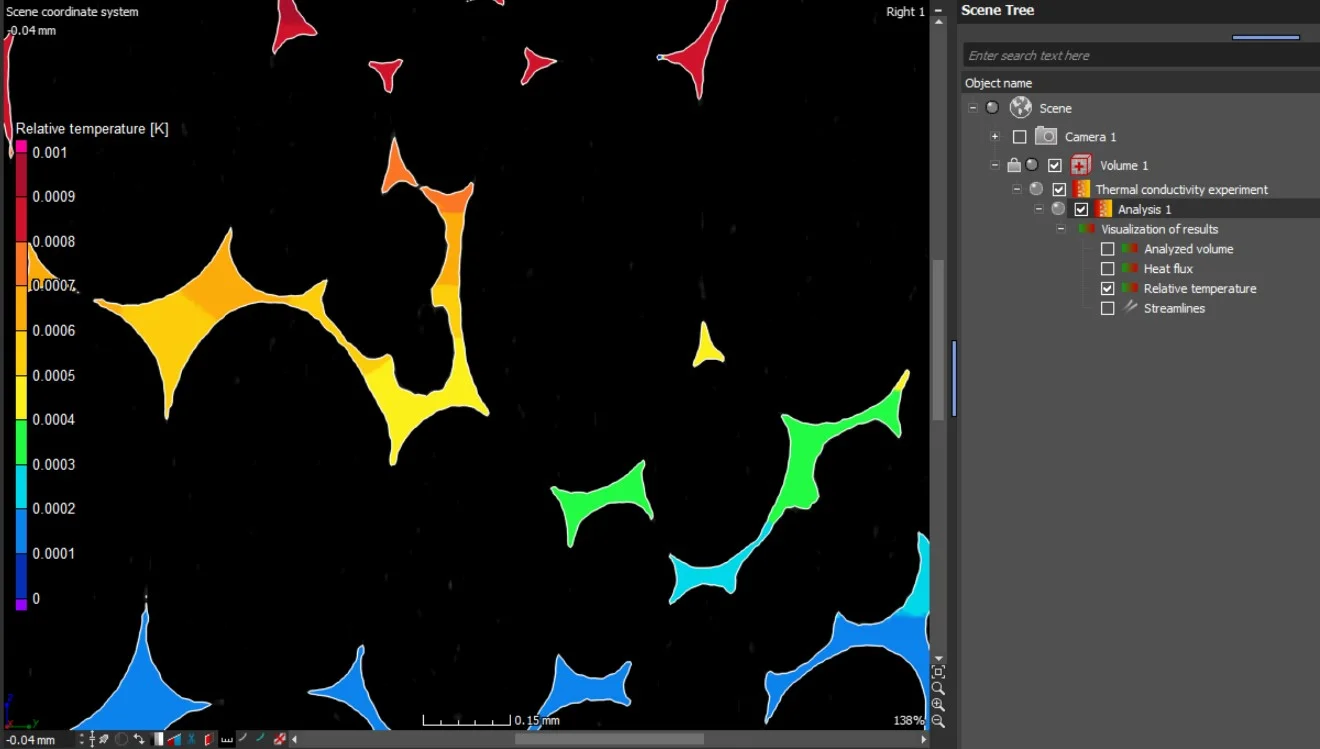
Calculation Results
The results are provided as 2D and 3D visualizations of the heat flux and the relative temperature. Heat flow directions can be visualized by streamlines in 2D and 3D:
- Heat flux
- Relative temperature
- Streamlines of heat flux
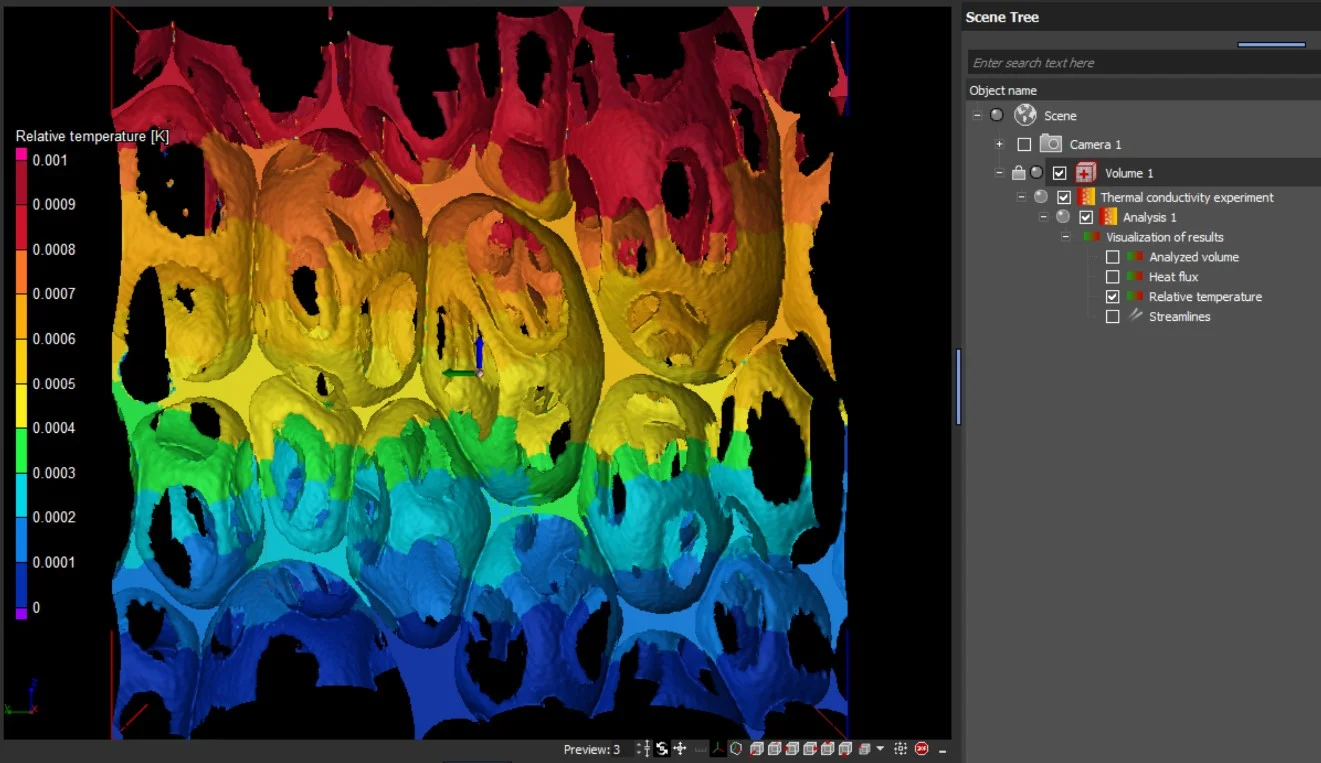
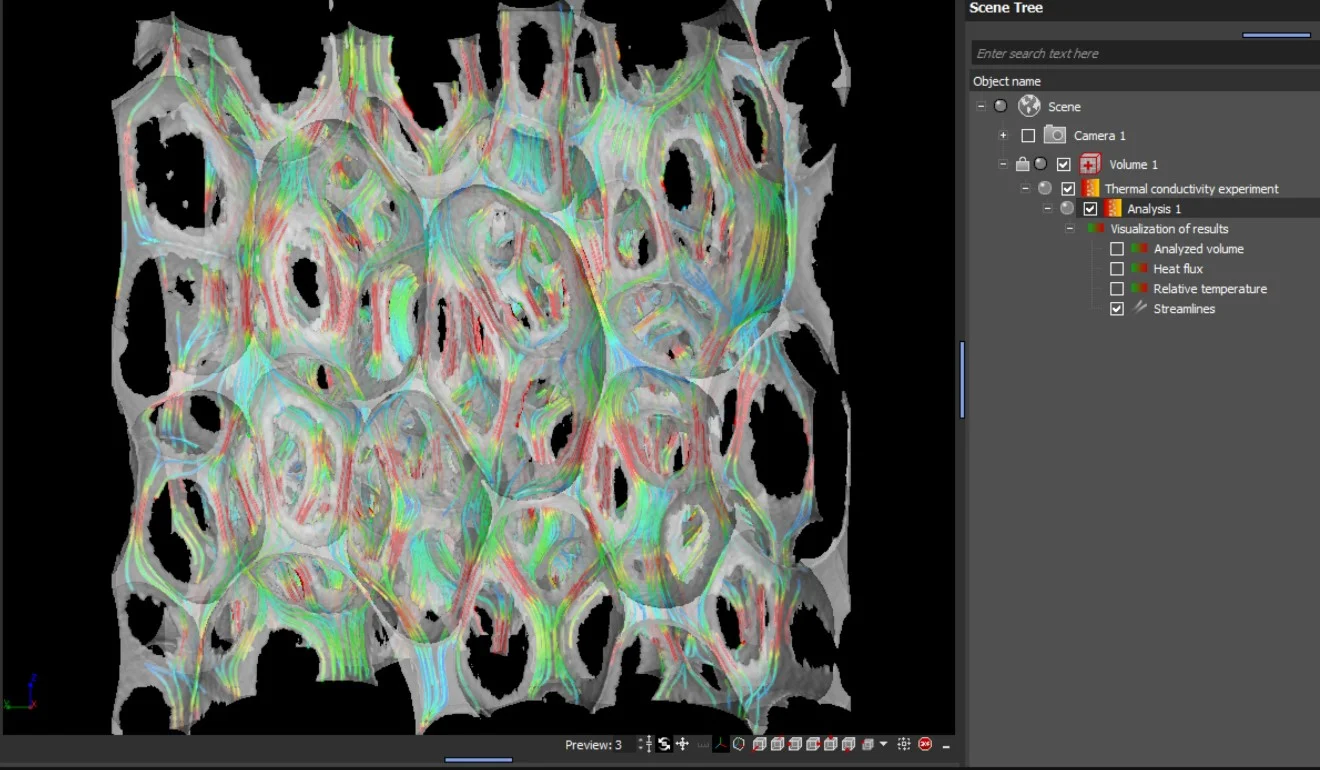
Additional Results
The following additional results are provided in a table view:
- Effective thermal conductivity
- Diffusive tortuosity (geometric and algebraic)
- Formation factor
- Void fraction
- Total heat transport
- Temperature gradient
The following results can be viewed as curve plots along the flow direction:
- Heat flux
- Void fraction
- Total heat transport
Tensor Mode
In tensor mode, the software calculates the effective tensor-valued thermal conductivity. The calculation of the thermal conductivity tensor can be done on the whole structure or for increments of the structure by means of an integration mesh.
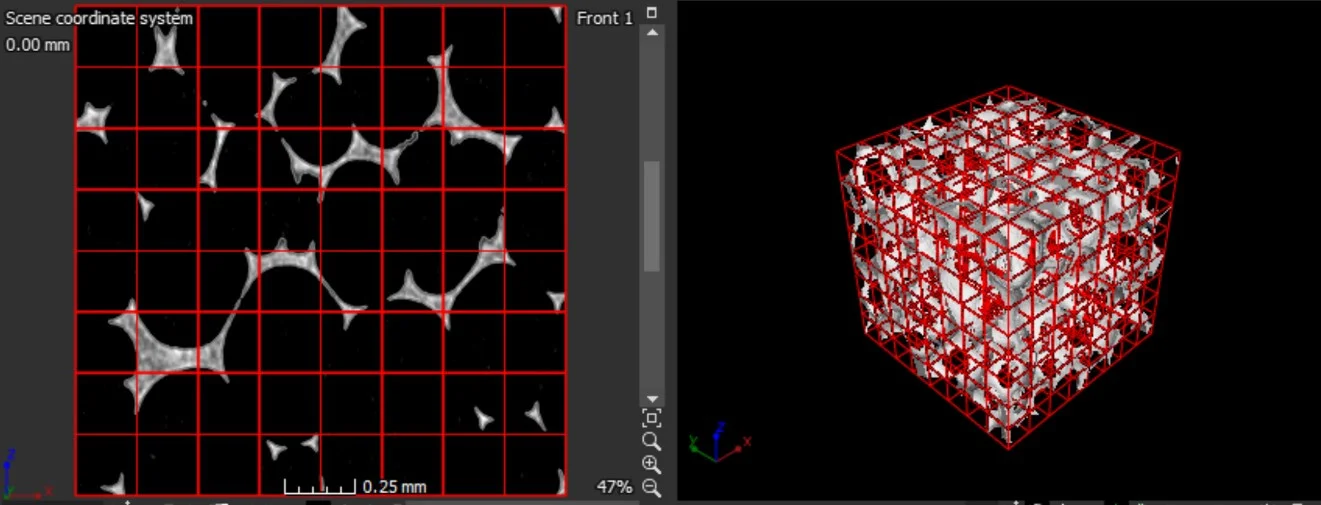
Results
The software provides thermal conductivity tensor results as 2D and 3D visualizations.
- Results are displayed as an ellipsoid in the center of the simulated volume.
- When the analysis is performed on an integration mesh, results are displayed as an ellipsoid in the center of each cell.
- The main axes of the ellipsoid are aligned with the eigenvectors of the tensor while the lengths of the axes are proportional to the eigenvalues of the tensor.
- When the analysis is performed on an integration mesh, the mean effective thermal conductivity and the void fraction as well as the eigenvalues of the thermal conductivity tensor can also be visualized in 2D and 3D.
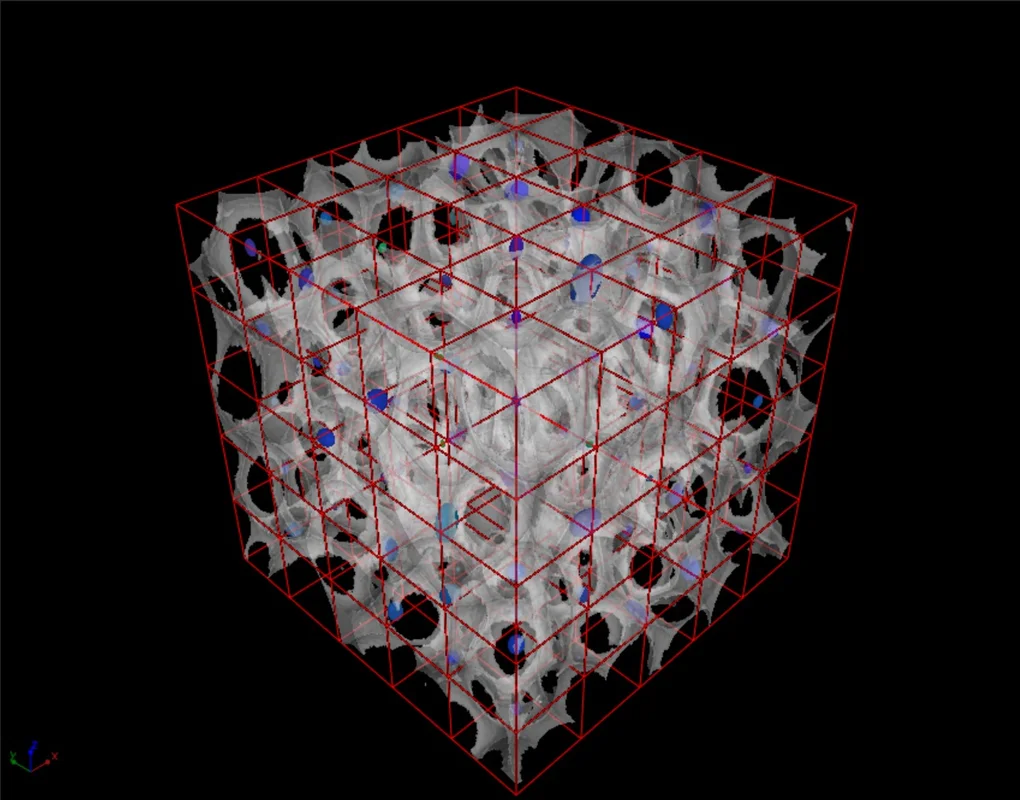
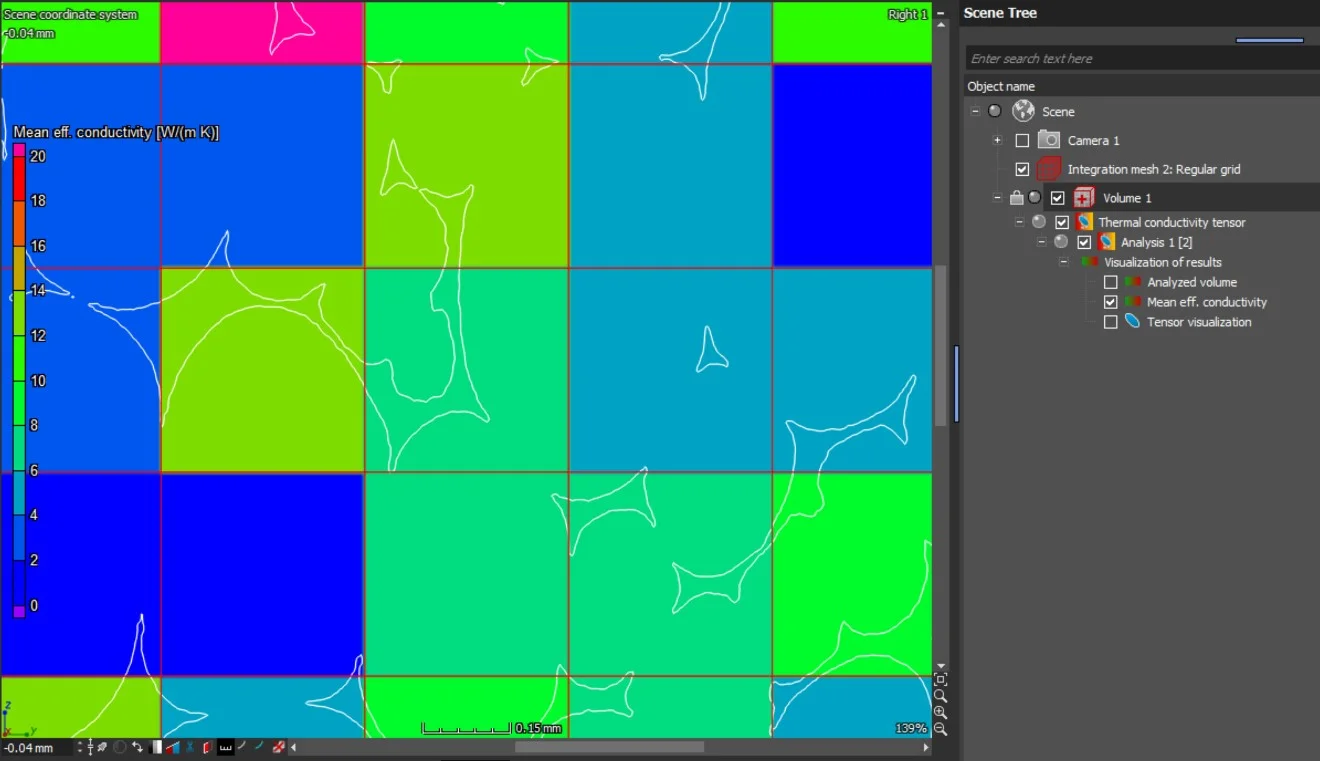
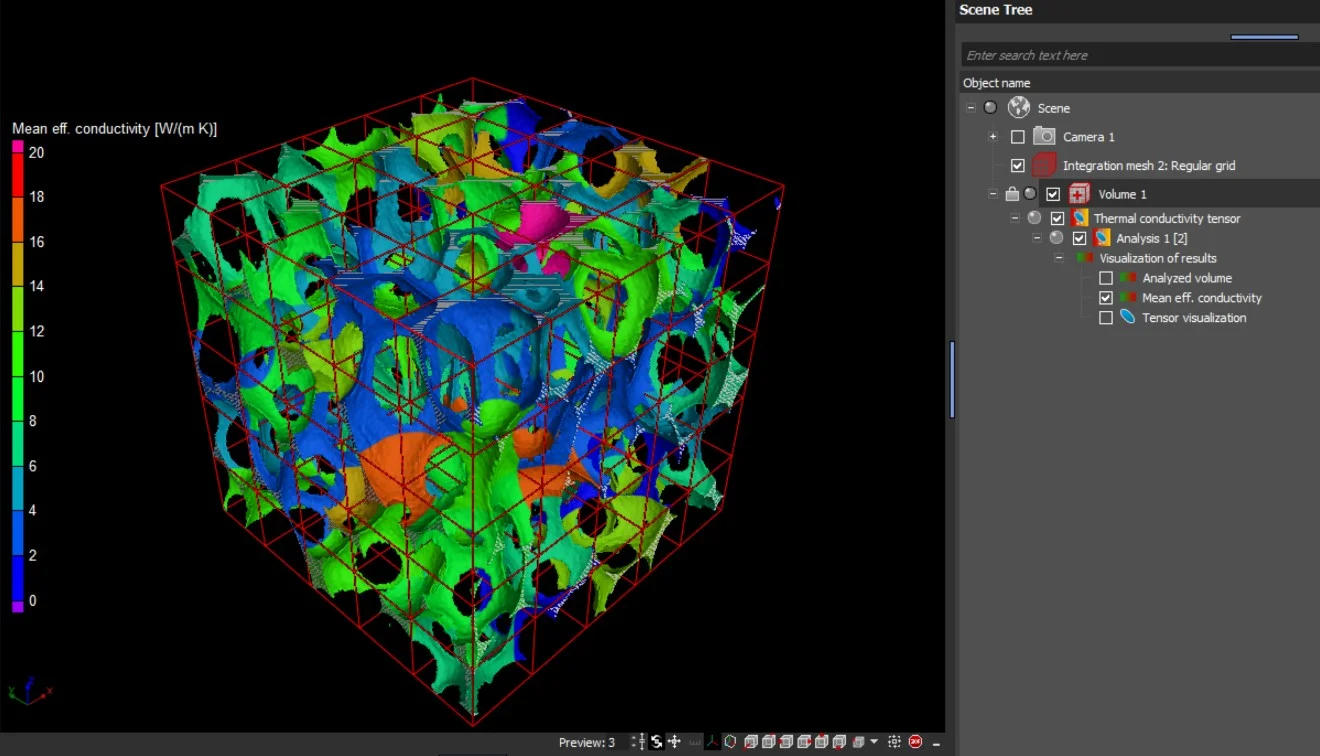
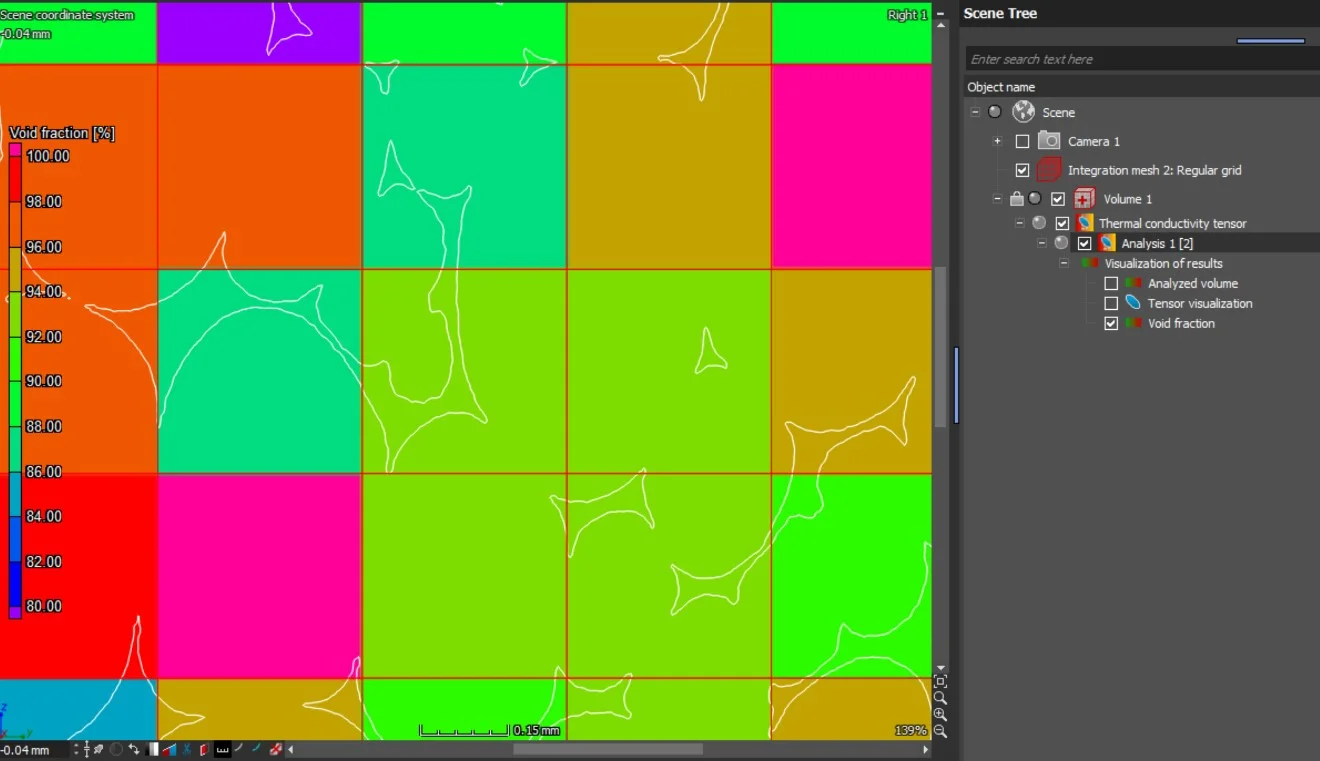
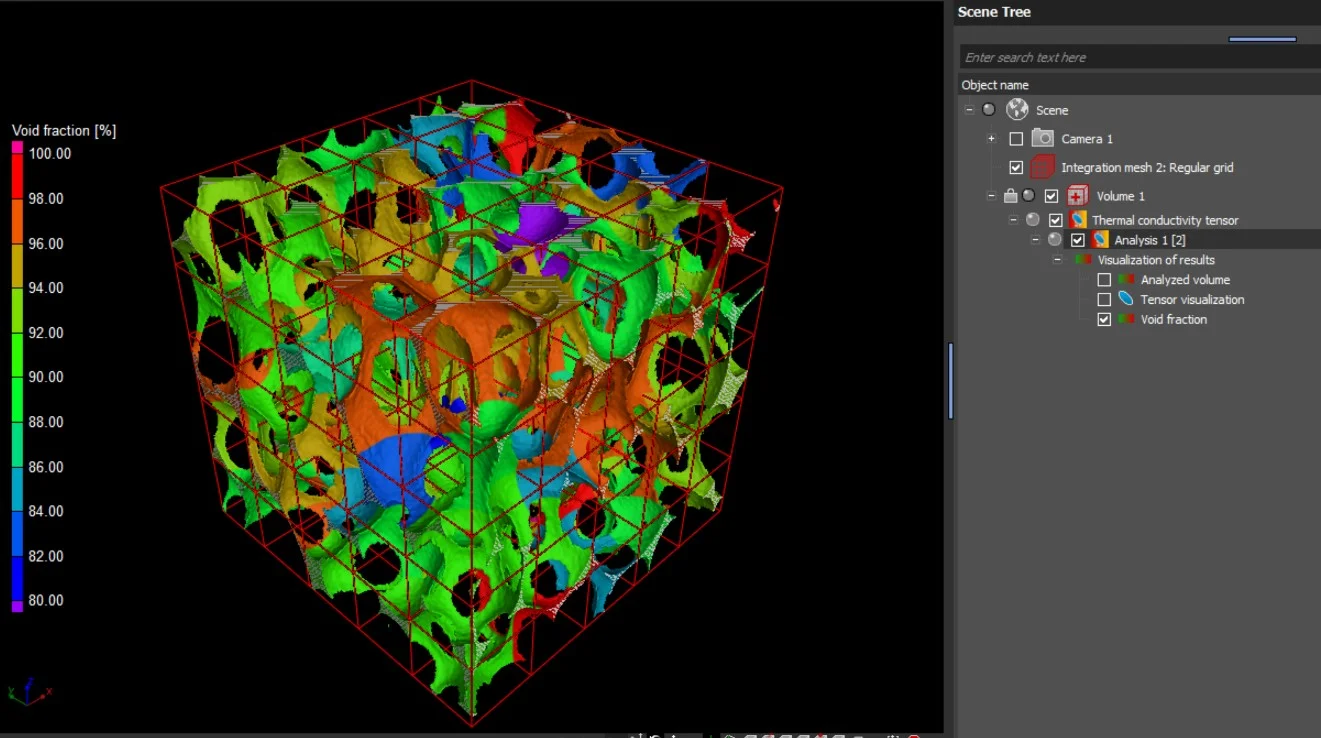
In addition to the tensors' eigenvalues and eigenvectors, the components of the effective thermal conductivity tensor with respect to the simulation coordinate system are provided in a table view.
Benefits
Easy to use
- No simulation expertise required
- No meshing required
Efficient
- Seamless workflow from material segmentation to simulation in one software
Realistic
- All microstructural details are captured by a subvoxel accurate surface determination